My approach to solving a domino jigsaw involves three basic steps:

Step 1. Select a domino (pair of numbers) and find a pair of numbers on the grid that is the only possible place that domino could go.

Step 2. Looking only at the grid, find two adjacent squares that must be a domino pair because they are hemmed in by other dominoes.

Step 3. Using the number pairs discovered in Step 2, block boundaries between unused numbers on the grid that match the Step-2 pairs.

For this particular puzzle, you have the advantage of seeing the actual dominoes and can use the orientation of some of them to further determine which is which.

Step 2 finds 1-6 in the lower left corner of the grid, because the square above the 6 is being used by the 0-0 tile.

Step 3 looks for any other 1-6 combination on the grid and draws a separator between the 1 and the 6 there. There is one such pair on the sixth row.

Then we repeat steps 1 through 3. Here is a table representing the actions we've taken so far:

The three steps have pretty much exhausted themselves, and the grid now looks like the diagram on the next page.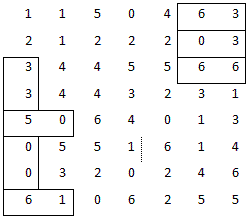

But in this puzzle we can see the spots on the dominoes; this gives us a new step.

Step 4. Split number pairs where the orientation of the spots doesn't match the sample dominoes pictured in the puzzle.

Can the 2-1 at the start of the second row be formed using the 1-2 tile? No. If those two numbers formed a tile, it would look like the first tile shown here, but the sample 1-2 tile looks like the second tile shown here. Split the first 1-2 on row 2.

The sixes, the threes, and the twos are asymmetric (that is, they don't look the same when they are rotated 90). If we split number pairs according to step 4, we get this grid: